运动除了直线运动和曲线运动两种运动形式外,还有一种运动形式是鼠标跟随运动,而这种跟随运动需要用到三角函数的相关内容或者需要进行比例运算。本文将以几个小实例来介绍角度运动的相关内容
眼球转动
在很多网页中,都存在着跟随运动,比如眼球转动。鼠标在网页中移动时,眼球也会跟着朝相应方向转动
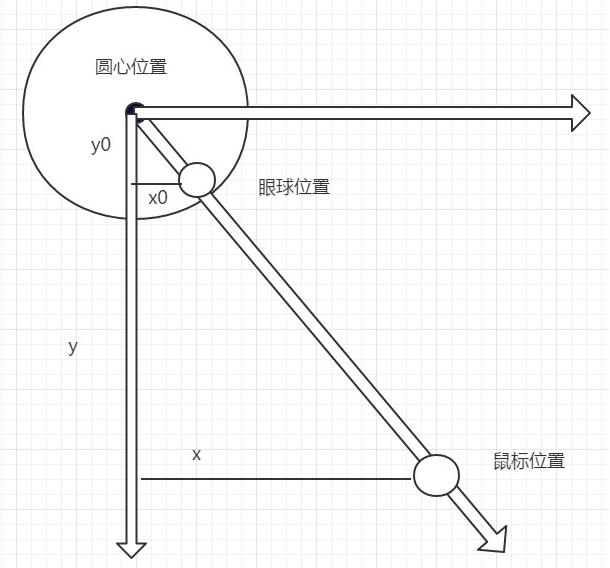
上面是眼球转动的示意图,(x0,y0)是眼球的位置,而(x,y)是鼠标的位置。设直线与垂直方向的夹角为a,假设圆心点坐标为(0,0),可以得到以下公式
tan(a) = x/y = x0/y0
x0 = r*sin(a)
y0 = r*cos(a)
在mousemove事件中,可以很容易的得到鼠标位置(x,y),由此求出夹角a,进而可以求出眼球的位置
设左眼为ball1,右眼为ball2。左眼的圆心坐标是(39,72),右眼的圆心坐标是(106,68),眼球可以移动的半径是12px
苹果菜单中也存在着鼠标跟随运动,与鼠标距离越近的菜单项的宽高越大,越远则宽高越小
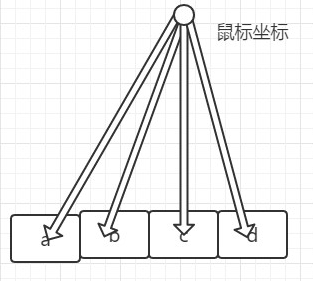
鼠标坐标可以通过mousemove事件中的clientX和clientY获得。菜单项的坐标其实是已知项。而鼠标坐标与菜单项的距离就是要求的距离,而距离与菜单项的宽高成反比
[注意]不能够将元素的自定义属性命名为x,因为x已经被浏览器使用
方向跟随
有许多网页都有方向跟随的效果。鼠标从哪个方向移入,元素就跟着从哪个方向移入。鼠标从哪个方向移出,类似地,元素也跟着从哪个方向移出
移入移出的运动效果使用匀速直线运动即可,这里主要需要判断方向
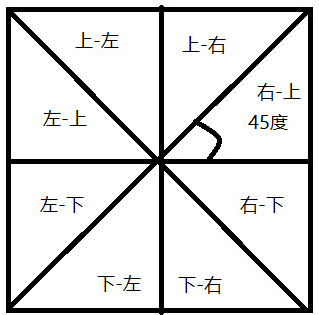
由示意图中所示,可以把一个正方形的元素分成(上-右、上-左、左-上、左-下、下-右、下-左、右-上、右-下)这8个部分,每个部分是一个等腰直角三角形,当元素进入某个区域时,横线前面的方向就表示元素的方向
假设正方形的中心坐标为(x0,y0),动态元素(move)进入时的坐标为(x,y),以这两个坐标组成的直线与水平正方向的直线的夹角作为基准角,假设为a,则通过确定夹角a的范围,可以确定动态元素(move)进入的方向



